Claim Your Discount Today
Celebrate the Christmas season with 15% OFF on all Statistics Homework Help at www.statisticshomeworkhelper.com ! 🎓 Let our expert statisticians handle your assignments with accurate solutions, clear explanations, and on-time delivery—so you can relax and enjoy the holidays without academic stress. 🎁 Use Christmas Offer Code: SHHRXMAS15 and make this festive season both joyful and productive!
We Accept
- 1. Understanding the Problem Statement
- 2. Maximum Likelihood Estimation (MLE)
- Steps to Derive MLE:
- 3. Evaluating Estimators: The Cramér-Rao Lower Bound (CRLB)
- Key Concepts:
- 4. Asymptotic Properties of Estimators
- 5. Order Statistics and Their Role in Estimation
- Important Considerations:
- 6. Identifiability and Uniqueness of Estimators
- Identifiability Conditions:
- 7. Common Pitfalls and Best Practices
- Conclusion
Statistical inference is a crucial area of study in statistics, focused on drawing conclusions about populations from sample data. Many students face challenges when dealing with assignments in this field, particularly those involving complex topics such as Maximum Likelihood Estimation (MLE), the Cramér-Rao Lower Bound, and order statistics. If you’re struggling with these concepts, seeking statistics homework help can provide much-needed guidance. A structured approach to statistical inference assignments ensures that students gain a solid theoretical understanding while minimizing the need for intricate computations. By focusing on key topics like MLE and CRLB, students can tackle even the most difficult statistical inference problems with confidence. Additionally, help with statistical inference homework often includes clarifying essential concepts like estimators, unbiased estimation, and asymptotic properties, enabling students to gain clarity and improve their problem-solving skills. Whether you’re analyzing sample distributions or deriving estimators, breaking down the problem into manageable steps is key to success in this challenging subject.

1. Understanding the Problem Statement
Understanding the problem statement is the first step in solving any statistical inference assignment. Carefully reading the problem allows you to identify key details, such as the type of estimator required (e.g., Maximum Likelihood Estimation or unbiased estimators), the underlying probability distribution (e.g., Normal or Poisson), and any regularity conditions that must be satisfied. By focusing on these elements, you can form a clear approach and determine which statistical methods or theorems to apply. Identifying the core concepts early on reduces the chances of making errors during the solution process and helps in crafting a precise, logically structured answer. Before solving any statistical inference assignment, the first step is to carefully analyze the problem statement. Typically, these assignments involve estimation, hypothesis testing, and asymptotic properties of estimators. Important considerations include:
- Identifying the type of estimator required (e.g., MLE, unbiased estimators).
- Determining the underlying probability distribution (e.g., Normal, Poisson, or Exponential families).
- Checking for regularity conditions that justify the use of key theorems.
2. Maximum Likelihood Estimation (MLE)
Maximum Likelihood Estimation (MLE) is a powerful statistical method used to estimate parameters by maximizing the likelihood function. This technique involves defining the likelihood of observing a given set of data under different parameter values and finding the parameter that maximizes this likelihood. The MLE is particularly valuable because it provides asymptotically efficient estimators, meaning that as sample sizes increase, the MLE approaches the true parameter value. By simplifying the differentiation process through the log-likelihood function, students can easily derive estimators and ensure optimality in their statistical analysis. MLE is foundational in statistical inference and widely used across various fields. MLE is one of the most powerful estimation techniques in statistics. It is based on maximizing the likelihood function, which represents the probability of observing the given data under different parameter values.
Steps to Derive MLE:
- Define the likelihood function: Given a sample Y1,Y2,…,Yn from a probability distribution with parameter θ, the likelihood function is:
- Compute the log-likelihood: Taking the logarithm simplifies differentiation:
- Differentiate and solve: The estimator θ^ is found by solving for θ in the following equation:
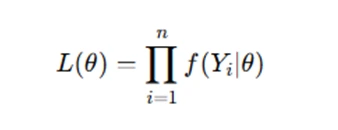
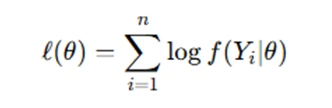
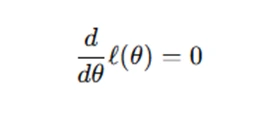
MLE provides asymptotically efficient estimators under regularity conditions, making it a cornerstone of statistical inference.
3. Evaluating Estimators: The Cramér-Rao Lower Bound (CRLB)
The Cramér-Rao Lower Bound (CRLB) is used to evaluate the efficiency of estimators. It provides a theoretical benchmark for the minimum variance that an unbiased estimator can achieve. The CRLB shows that an estimator with lower variance than the bound is considered efficient. It relies on the Fisher Information, which quantifies the amount of information that a sample provides about a parameter. In assignments, evaluating whether an estimator achieves the CRLB is essential to ensure that the estimator is optimal and that the solution is accurate. This concept is critical when determining whether a statistical method is the best approach for a given problem. One fundamental question in statistics is whether an estimator is efficient, meaning it has the lowest possible variance among all unbiased estimators. The Cramér-Rao Lower Bound provides a benchmark for variance.
Key Concepts:
- The Fisher Information measures the amount of information a sample contains about a parameter:
- The CRLB states that for any unbiased estimator θ^\hat{\theta}, its variance satisfies:
- If an estimator achieves the CRLB, it is considered an efficient estimator.
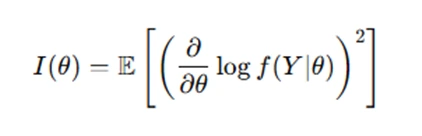
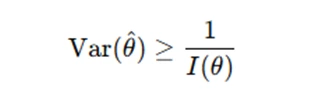
Checking whether an estimator attains the CRLB is crucial for evaluating its optimality in statistical assignments.
4. Asymptotic Properties of Estimators
Asymptotic properties of estimators become increasingly important in large-sample settings. As the sample size increases, estimators exhibit properties like consistency and asymptotic normality. Consistency means that the estimator converges to the true parameter value as the sample size grows. Asymptotic normality indicates that the distribution of an estimator approaches a normal distribution in large samples. These properties help justify the use of methods like Maximum Likelihood Estimation (MLE) in practice, especially in cases where large data sets are involved. Understanding these properties aids in evaluating the long-term behavior of estimators. Many statistical inference assignments focus on asymptotic results, particularly the behavior of estimators as sample size n→∞.
Important results include:
- Consistency: An estimator θ^n is consistent if it converges to the true parameter value as n→∞:
- Asymptotic Normality: Under certain regularity conditions, the distribution of an estimator approaches a normal distribution as n→∞n:
- Asymptotic Efficiency: An estimator is asymptotically efficient if it achieves the Cramér-Rao Lower Bound (CRLB) asymptotically:
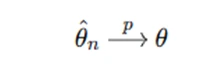 (in probability).
(in probability).
This means that for any
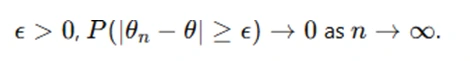
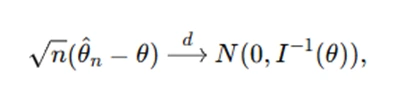
where I(θ) is the Fisher Information.
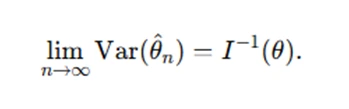
These properties help justify the use of MLE in large-sample settings.
5. Order Statistics and Their Role in Estimation
Order statistics are statistics that involve the ranking of sample data, such as the smallest, largest, or middle values in a sample. These statistics play an essential role in estimating parameters, especially when dealing with extreme values or analyzing the distribution of sample data. In statistical inference, order statistics are used in methods like minimum variance unbiased estimation (UMVUE) and likelihood-based estimation. The study of order statistics helps in solving complex problems by providing insights into the sample's structure, which is critical when deriving estimators for population parameters. Understanding their behavior and applications enhances the ability to tackle real-world problems effectively. Order statistics arise frequently in assignments, particularly when analyzing sample extremes or distributions of ranked observations.
Important Considerations:
- The k-th order statistic, Y(k) represents the k-th smallest value in a sample of size n, such that Y(1)≤Y(2)≤⋯≤Y(n).
- The distribution of order statistics plays a key role in minimum variance unbiased estimation (UMVUE) problems. For instance, the expected value of the k-th order statistic for a uniform distribution is given by:
- Some estimators based on order statistics may not be sufficient, meaning they do not capture all available information about the parameter. For example, the median order statistic Y([n/2]) may not be sufficient for estimating the mean of a distribution in certain cases.
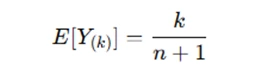
Understanding order statistics is essential when solving problems related to MLE, sufficiency, and likelihood-based estimation.
6. Identifiability and Uniqueness of Estimators
Identifiability refers to the ability to determine a unique set of parameters from a probability distribution. An estimator is identifiable if different parameter values produce distinct probability distributions. This concept is crucial because an estimator that is not identifiable could lead to multiple possible solutions, making it difficult to draw accurate conclusions. Some models, such as mixture models, may present identifiability challenges that require constraints or reparameterization. Identifiability ensures that the parameters being estimated are meaningful and that the solution to a statistical problem is unique and reliable. Properly addressing identifiability is a key step in statistical inference assignments. Identifiability is a crucial concept in statistical modeling. An estimator must be identifiable to ensure unique parameter estimation.
Identifiability Conditions:
- A model is identifiable if different parameter values lead to distinct probability distributions.
- Some models, such as mixture models, pose identifiability challenges, requiring additional constraints or reparameterization.
- Assignments often require proving whether a given likelihood function uniquely determines the parameters.
Checking identifiability ensures the meaningfulness of an estimator in statistical inference problems.
7. Common Pitfalls and Best Practices
When working on statistical inference assignments, there are several common pitfalls to avoid. These include ignoring regularity conditions, misinterpreting the likelihood function, and failing to account for asymptotic properties. Students often overlook conditions that are necessary for certain theorems to hold, such as differentiability and existence of expectations. It’s also easy to incorrectly specify the likelihood, leading to inaccurate estimators. Another common mistake is misunderstanding the difference between sufficiency and efficiency. To overcome these challenges, students should carefully check all assumptions, verify the conditions for key theorems, and apply a structured, methodical approach to the solution process. Solving statistical inference assignments requires careful attention to detail. Some common pitfalls include:
- Ignoring regularity conditions: Many theorems (e.g., MLE consistency, CRLB) require assumptions about differentiability and existence of expectations.
- Misinterpreting likelihood functions: Incorrectly specifying the likelihood leads to erroneous estimators.
- Overlooking asymptotic properties: Many results hold only for large samples; failing to check sample size constraints can lead to incorrect conclusions.
- Confusing sufficiency and efficiency: A sufficient statistic captures all data information but may not be the most efficient estimator.
To avoid these issues, students should verify conditions, check assumptions, and follow a structured approach when deriving and evaluating estimators.
Conclusion
Statistical inference assignments, particularly those involving MLE, CRLB, order statistics, and asymptotic properties, require a rigorous theoretical approach. By carefully analyzing problem statements, applying core estimation principles, and checking key statistical properties, students can develop precise and well-reasoned solutions. Following a structured methodology ensures not only correctness but also deeper comprehension of statistical inference techniques.
.webp)








