Claim Your Discount Today
Get 10% off on all Statistics Homework at statisticshomeworkhelp.com! This Spring Semester, use code SHHR10OFF to save on assignments like Probability, Regression Analysis, and Hypothesis Testing. Our experts provide accurate solutions with timely delivery to help you excel. Don’t miss out—this limited-time offer won’t last forever. Claim your discount today!
We Accept
- 1. Understanding the Basics of Probability
- 2. Analyzing the Problem Statement
- 3. Organizing Data Effectively
- A. Contingency Tables
- B. Tree Diagrams
- 4. Addressing Key Probability Questions
- A. Marginal Probabilities
- B. Joint Probabilities and Independence
- C. Conditional Probabilities
- D. Conditional Distributions
- 5. Strategies for Effective Problem Solving
- A. Break Down the Problem
- B. Cross-Check Calculations
- C. Justify Your Answers
- 6. Common Challenges and How to Overcome Them
- A. Misinterpreting Data
- B. Calculation Errors
- C. Misunderstanding Independence
- 7. Leveraging Statistical Software
- Conclusion
Probability assignments can be daunting, often requiring students to analyze complex scenarios involving calculations of probabilities, conditional probabilities, event independence, and contingency tables. For those seeking clarity and efficiency, leveraging statistics homework help can be a game-changer. This essential support not only simplifies understanding but also enhances problem-solving accuracy by breaking down intricate concepts into manageable steps. By focusing on theoretical foundations and practical strategies, such as organizing data into contingency tables or tree diagrams, students can confidently address problems like conditional probabilities or event independence. Additionally, accessing professional help with probability homework enables students to approach their assignments methodically, ensuring they grasp critical principles while saving time on tedious calculations. With a structured approach, a clear understanding of concepts, and the right resources, mastering probability becomes less about struggle and more about building analytical confidence and achieving academic success.
1. Understanding the Basics of Probability

To succeed in probability assignments, it's crucial to have a strong understanding of fundamental concepts. Probability measures how likely an event is to occur. Essentially, it is determined by dividing the number of favorable outcomes by the total number of possible outcomes. Conditional probability, on the other hand, calculates the likelihood of an event occurring given that another event has already occurred. This concept helps to refine the probability based on the occurrence of another event. Independence refers to the relationship between two events where the occurrence of one does not affect the likelihood of the other. In other words, if two events are independent, knowing the outcome of one event does not change the probability of the other event happening. Complementary events are those where the probability of an event not happening is simply one minus the probability of the event occurring. These core principles provide the foundation needed to tackle more complex probability problems. Before solving any probability-based assignment, it is essential to grasp these basic concepts and understand how they interconnect. Before solving any probability-based assignment, it is essential to grasp the fundamental concepts:
- Probability: A measure of the likelihood of an event occurring, expressed as:
- Conditional Probability: The probability of an event occurring given that another event has already occurred, represented as:
- Independence: Two events are independent if:
- Complementary Events: The probability that an event does not occur is:
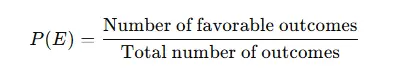
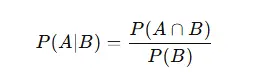
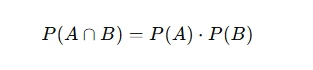
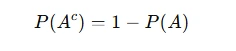
These core concepts serve as building blocks for analyzing more complex scenarios.
2. Analyzing the Problem Statement
Careful analysis of the problem statement is crucial to solving probability problems accurately. Start by identifying the given data, such as probabilities, sample sizes, and any relevant distributions. Understanding the type of problem—whether it involves conditional probability, independence, or joint probability—is vital for selecting the correct approach. It is also essential to determine the required outcomes, such as calculating specific probabilities or comparing events. Thoroughly analyzing the problem statement ensures that the right techniques and formulas are applied, preventing mistakes and streamlining the solution process. Carefully read and dissect the problem statement. Identify:
- The given data (e.g., probabilities, total sample size, distributions).
- The type of problem (e.g., conditional probability, independence, or joint probability).
- The required outcomes (e.g., specific probabilities or comparisons).
In the provided assignment, questions such as calculating P(F) and P(C), and analyzing conditional probabilities (P(F∣C), P(C∣F), focus on interpreting and applying probability principles.
3. Organizing Data Effectively
Organizing data systematically is one of the most effective ways to approach probability problems. Tools like contingency tables and tree diagrams are invaluable for visually mapping out relationships and events. Contingency tables can show how different categories relate to each other, making it easier to compute marginal, joint, and conditional probabilities. For example, a table may present the distribution of eye colors by gender, from which probabilities such as P(F) (probability of being female) or P(C∣F) (probability of having green eyes given that the person is female) can be calculated. Tree diagrams, on the other hand, are useful for modeling sequential events, displaying probabilities for each branch, and helping with the calculation of conditional probabilities. Proper organization of data simplifies complex calculations and reduces the risk of errors, making it an essential skill in probability problem-solving. Organizing data into tables or diagrams can significantly simplify problem-solving. Use the following tools:
A. Contingency Tables
Contingency tables help visualize relationships between categorical variables. For instance:
| Gender \ Eye Color | Blue Eyes | Brown Eyes | Green Eyes | Hazel Eyes | Total |
|---|---|---|---|---|---|
| Female | a | b | c | d | F |
| Male | e | f | g | h | M |
| Total | A | B | C | D | N |
- Calculate marginal totals and conditional probabilities for analysis.
- For example:
For example:
P(F)=F/N
P(C∣F)= (c/F)
B. Tree Diagrams
Tree diagrams are valuable for conditional probabilities, particularly when dealing with sequential events.
- Start with initial probabilities (e.g., gender distribution).
- Branch out into conditional probabilities (e.g., eye color given gender).
4. Addressing Key Probability Questions
In probability assignments, addressing key questions involves applying core principles like marginal, joint, and conditional probabilities. Marginal probabilities, such as P(F) (the probability of being female), can be easily calculated from a contingency table by dividing the relevant frequency by the total population. Joint probabilities, such as P(F∩C) (the probability of being female and having green eyes), assess the likelihood of two events happening simultaneously. For testing independence, the formula P(F∩C)=P(F)⋅P(C) is used; if the equality holds, the events are independent. Conditional probabilities, such as P(F∣C) (the probability of being female given green eyes), help determine the likelihood of one event occurring in the context of another. These essential concepts enable students to approach and solve various probability problems methodically.
A. Marginal Probabilities
Calculate basic probabilities like P(F) (probability of being female) or P(C) (probability of having green eyes) using frequencies from the contingency table.
B. Joint Probabilities and Independence
Determine P(F∩C)P (probability of being female and having green eyes) to assess independence. Use:
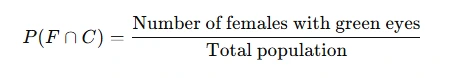
Check for independence using the formula:
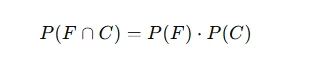
If equality holds, the events are independent.
C. Conditional Probabilities
Focus on questions like:
- P(F∣C): The probability of being female given green eyes.
- P(C∣F): The probability of having green eyes given being female.
These probabilities are computed as:
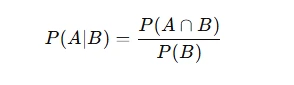
D. Conditional Distributions
Examine the distribution of eye colors within genders:
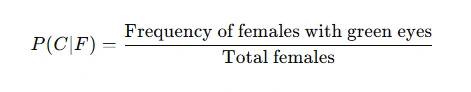
Compare distributions across categories to identify trends or differences.
5. Strategies for Effective Problem Solving
Effective problem-solving in probability requires a structured approach. Start by breaking down complex problems into smaller, manageable parts, such as calculating basic probabilities first and then advancing to joint or conditional probabilities. This strategy prevents feeling overwhelmed and allows for a step-by-step progression toward the solution. It's also crucial to cross-check calculations, ensuring that the sum of all probabilities equals 1 and using complementary probabilities where applicable. Additionally, justification of answers is important; clearly explain reasoning, especially when determining independence or comparing distributions. Supporting claims with accurate calculations and interpretations builds a stronger, more reliable solution. These strategies ensure that students can approach probability assignments with confidence and accuracy.
A. Break Down the Problem
Split complex questions into smaller, manageable parts. For example:
- Calculate basic probabilities first (e.g., P(F),P(C)).
- Move on to joint and conditional probabilities.
- Analyze independence and distributions.
B. Cross-Check Calculations
Verify calculations by:
- Summing probabilities to ensure they equal 1.
- Using complementary probabilities where applicable.
C. Justify Your Answers
Explain reasoning clearly, especially when assessing independence or comparing distributions. Support claims with calculations and interpretations.
6. Common Challenges and How to Overcome Them
While working through probability problems, students often face challenges such as misinterpreting data, making calculation errors, or misunderstanding independence. To avoid misinterpretation, it’s crucial to carefully read the problem statement and data tables, ensuring all events and outcomes are correctly identified. Calculation errors can be minimized by consistently using the correct formulas and double-checking computations for accuracy. Misunderstanding independence can lead to incorrect conclusions, so it’s important to remember that independence between two events means P(A∩B)=P(A)⋅P(B). Careful analysis of event relationships and a firm understanding of the independence concept will help avoid such pitfalls. By recognizing these common challenges and implementing the right strategies, students can overcome obstacles and successfully solve probability problems.
A. Misinterpreting Data
- Double-check problem statements and data tables.
- Ensure accurate identification of events and outcomes.
B. Calculation Errors
- Use consistent formulas.
- Recheck computations to avoid mistakes.
C. Misunderstanding Independence
- Remember that independence requires P(A∩B)=P(A)P(B).
- Carefully analyze relationships between events.
7. Leveraging Statistical Software
While theoretical understanding is crucial for solving probability problems, leveraging statistical software can significantly enhance the problem-solving process. Tools such as Excel, R, or Python provide powerful capabilities for organizing data, performing calculations, and visualizing probabilities. For instance, Excel is helpful for creating contingency tables and calculating basic probabilities, while R or Python can be used for more complex analyses, such as creating probability distributions or testing for event independence. Statistical software can automate tedious calculations, reduce human error, and provide quick, accurate results. While understanding the underlying theory is essential, utilizing statistical software enhances efficiency and precision, making it a valuable tool for students tackling probability assignments.While the focus here is theoretical, tools like Excel, R, or Python can simplify computations and visualization:
- Use Excel for contingency tables and basic probability calculations.
- Leverage R or Python for complex analyses, such as creating distributions or testing independence.
Conclusion
Solving probability assignments requires a clear understanding of concepts, organized data representation, and a systematic approach. By breaking down problems, leveraging tools like contingency tables and tree diagrams, and verifying calculations, students can confidently tackle even the most challenging questions. These strategies provide a robust framework for analyzing probabilities, conditional probabilities, and event independence, ensuring academic success.
.webp)








