Claim Your Discount Today
Get 10% off on all Statistics Homework at statisticshomeworkhelp.com! This Spring Semester, use code SHHR10OFF to save on assignments like Probability, Regression Analysis, and Hypothesis Testing. Our experts provide accurate solutions with timely delivery to help you excel. Don’t miss out—this limited-time offer won’t last forever. Claim your discount today!
We Accept
- Understanding the Problem Statement
- Hypothesis Formulation
- Data Preparation and Exploration
- Choosing the Appropriate Statistical Test
- Hypothesis Testing Steps
- Confidence Intervals
- Interpreting Results
- Practical Application
- Common Pitfalls and Tips
- Conclusion
Statistical assignments often pose challenges that demand a thorough grasp of theoretical concepts, critical analysis, and the systematic application of statistical methods. Whether you’re evaluating airport performance through canceled flights, analyzing bad debt ratios in banking, or determining lead concentration levels in water, a structured approach is crucial for success. This blog explores the core methodologies to tackle such tasks effectively, emphasizing hypothesis testing, confidence interval estimation, and clear statistical interpretation. By focusing on understanding the problem, defining hypotheses, and using appropriate statistical tools, you can navigate through assignments with confidence. At its core, statistical problem-solving is about connecting data to meaningful conclusions while maintaining accuracy and clarity. With statistics homework help, students can gain the expertise needed to demystify even the most intricate problems and develop the critical thinking skills essential for academic excellence. From framing null and alternative hypotheses to interpreting results within a real-world context, this guide provides a roadmap for approaching statistical challenges with precision and confidence.
Understanding the Problem Statement

Every statistical assignment begins with understanding the problem statement. A clear interpretation of what is being analyzed—be it flight cancellations, financial ratios, or environmental safety thresholds—is crucial. This step involves identifying the key variables, the context of the data, and the ultimate question being addressed. For instance, does the data seek to compare proportions, test means, or assess trends? Clarity at this stage ensures that subsequent steps align with the objective, saving time and avoiding misinterpretation.The first step in solving any statistical assignment is to thoroughly understand the problem. Key aspects to focus on include:
- Identifying Variables: Differentiate between dependent and independent variables. For example, in the flight cancellation scenario, the dependent variable could be the proportion of canceled flights, while the independent variable might be the airport.
- Recognizing the Objective: Determine if the assignment requires hypothesis testing, confidence interval estimation, or another statistical analysis.
- Understanding Context: Contextualize the data to make meaningful interpretations. For instance, knowing that flight cancellations might vary by season or weather conditions is essential.
Hypothesis Formulation
Once the problem is understood, the next step is hypothesis formulation. This involves framing the null and alternative hypotheses. The null hypothesis generally represents no effect or no difference, while the alternative reflects the specific claim being tested. For example, in evaluating flight cancellations, the null could state that the proportion of canceled flights at an airport is the same as the national average, with the alternative suggesting otherwise. Precision here lays the foundation for valid conclusions. Hypotheses form the foundation of statistical analysis. Typically, you’ll need to state:
- Null Hypothesis (H₀): Represents no effect or no difference. For example, "The proportion of canceled flights at O'Hare Airport is equal to the national average."
- Alternative Hypothesis (Hᵣ): Represents the claim being tested, such as "The proportion of canceled flights at O'Hare Airport is different from the national average."
When formulating hypotheses, be clear and precise. Use mathematical notations like p=p0p = p_0 for clarity when referring to proportions.
Data Preparation and Exploration
Data preparation ensures reliability. This includes cleaning datasets, checking for missing values, and summarizing data through descriptive statistics and visualizations. Patterns, anomalies, or distributions observed at this stage inform the choice of statistical tests and enhance understanding. Proper exploration bridges raw data and meaningful analysis. Before analysis, data must be cleaned and prepared. Key steps include:
- Handling Missing Values: Decide whether to exclude or impute missing data based on the context and data size.
- Exploratory Data Analysis (EDA): Use graphical methods like histograms or box plots and summary statistics (mean, median, standard deviation) to understand data distribution.
- Outlier Identification: Identify any extreme values that might skew results.
For example, in the canceled flights dataset, summarize the total and airport-specific cancellation rates to provide insights before diving into hypothesis testing.
Choosing the Appropriate Statistical Test
Selecting the right test is critical and depends on the data type and hypothesis. For proportions, a z-test might be appropriate; for means, a t-test; and for categorical data, a chi-square test. Each test has assumptions, like normality or sample size, which must be verified to ensure validity. Selecting the right statistical test depends on the data type and objective. Common scenarios include:
- Proportion Tests: When comparing proportions, as in the O'Hare cancellation scenario, use a one-sample or two-sample proportion z-test.
- Mean Comparisons: For comparing means, as in the bad debt ratio example, use a t-test (one-sample or two-sample).
- Chi-Square Tests: For categorical data, such as determining if movie ratings meet a threshold, apply a chi-square test for independence or goodness-of-fit.
Ensure assumptions of the chosen test (e.g., normality, independence) are met before proceeding.
Hypothesis Testing Steps
Hypothesis testing follows a structured process: setting a significance level (commonly 5%), calculating the test statistic, and comparing it to critical values or p-values. The decision to reject or fail to reject the null is then based on this comparison. Finally, the result is interpreted in the context of the problem, providing actionable insights grounded in data. Follow these steps for effective hypothesis testing:
- State Hypotheses: Clearly define H₀ and Hᵣ.
- Select Test Statistic: Identify the appropriate test statistic based on the problem (e.g., z-score, t-score).
- Determine Significance Level (α): Commonly set at 0.05.
- Calculate Test Statistic: Apply the formula for the test statistic. For example, the z-test for proportions is:
- p^ = sample proportion
- p0 = population proportion under the null hypothesis
- n = sample size
- Find p-value or Critical Value: Compare the test statistic to the critical value or use the p-value approach.
- Draw Conclusions: Reject H₀ if the p-value is less than α, otherwise fail to reject H₀.
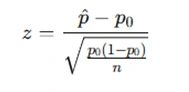
Where:
Confidence Intervals
Confidence intervals are crucial in statistical analysis as they provide a range within which a population parameter is likely to fall. For example, when evaluating the proportion of canceled flights or bad debt ratios, confidence intervals help quantify the uncertainty around sample estimates. Constructing these intervals involves determining the margin of error based on the chosen confidence level, typically 95%. This allows analysts to make informed decisions while acknowledging variability. By understanding how to calculate and interpret confidence intervals, students can effectively present reliable conclusions in their assignments. For the O'Hare scenario, the 95% confidence interval for the proportion of canceled flights can be calculated as:
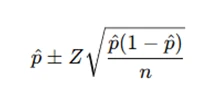
Where:
- p^ is the sample proportion (e.g., the proportion of canceled flights).
- Z is the critical value for the desired confidence level (e.g., 1.96 for 95% confidence).
- n is the sample size (e.g., the total number of flights in the sample).
Confidence intervals complement hypothesis testing by offering additional insights into the data.
Interpreting Results
Interpreting results is the bridge between statistical computation and practical understanding. After conducting hypothesis tests or calculating confidence intervals, it’s essential to contextualize the findings. For instance, determining whether Chicago O’Hare Airport’s cancellation rate significantly deviates from the national average requires translating p-values or confidence intervals into actionable insights. Clear interpretation ensures that results are meaningful and aligned with the objectives of the analysis. Interpretation bridges the gap between statistical findings and real-world implications. For example:
- Hypothesis Testing: If the p-value is less than 0.05, conclude that there is sufficient evidence to suggest a difference in cancellation rates.
- Confidence Intervals: If the interval does not include the null value, it supports the alternative hypothesis.
Relate statistical conclusions to the context, ensuring that non-technical audiences can understand their significance.
Practical Application
Statistical assignments are more than calculations—they connect theoretical knowledge with real-world scenarios. Whether it’s assessing water safety levels or evaluating financial metrics, the practical application of statistical tools ensures that data-driven insights lead to informed decisions. Emphasizing relevance strengthens problem-solving skills and highlights the utility of statistics in various fields. Applying these principles to assignments:
- Canceled Flights Analysis: Compare proportions of cancellations between airports or over time to identify patterns.
- Bad Debt Ratios: Test whether Illinois banks have higher debt ratios than the Midwestern average.
- Movie Ratings: Assess whether movies meet a retention threshold using one-sample tests.
- Water Safety: Evaluate lead concentrations to determine if water is safe based on regulatory thresholds.
Common Pitfalls and Tips
Statistical assignments often encounter errors such as misinterpreting results or misapplying formulas. Avoiding these pitfalls requires attention to detail, understanding underlying assumptions, and verifying computations. Tips like breaking complex problems into smaller steps, double-checking calculations, and seeking "statistics homework help" can significantly improve accuracy and comprehension. Avoid these common mistakes when working on statistical assignments:
- Misinterpreting Hypotheses: Clearly distinguish between H₀ and Hᵣ.
- Ignoring Assumptions: Validate assumptions like normality or sample independence before testing.
- Overcomplicating Analysis: Focus on the relevant statistical methods without unnecessary complexity.
Tips for success:
- Visualize data to identify trends and anomalies.
- Double-check calculations and rounding rules.
- Provide clear, concise explanations for your findings.
Conclusion
Statistical assignments provide an excellent opportunity to hone critical thinking and data analysis skills by bridging theoretical concepts with practical applications. Tasks such as analyzing airline performance, financial metrics, or safety standards require a structured approach involving hypothesis testing, confidence intervals, and result interpretation. Success in these assignments depends on clarity, precision, and the ability to translate statistical findings into actionable insights. Avoiding common pitfalls like misapplying methods or neglecting assumptions is key, and seeking resources like statistics homework help can offer valuable guidance. These assignments not only enhance academic performance but also equip students with skills vital for making informed, data-driven decisions in real-world scenarios. By focusing on clear methodologies and practical relevance, students can tackle statistical challenges confidently and effectively, paving the way for both academic and professional success.









