Approaching Statistical Assignments with Regression and Estimation Techniques

When approaching a statistical assignment, the first step is to carefully understand the problem statement. Identify key variables, their relationships, and the objectives of the analysis. For instance, distinguishing between dependent and independent variables sets the foundation for further analysis. Clearly defining the problem ensures that all subsequent steps are aligned with the intended outcomes. The first step in tackling any statistical assignment is to thoroughly comprehend the requirements. Assignments like the one provided typically involve:

Mean Calculation

The mean of a dataset is the central value and is computed as:

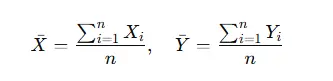
This forms the basis for further calculations, including variances and covariances.

Variance and Standard Deviation

Variance measures data dispersion and is calculated as:

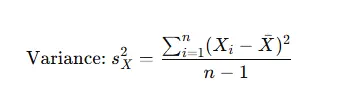
The square root of the variance gives the standard deviation :

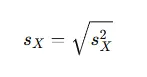
These metrics quantify the spread of the data around the mean.

2. Covariance and Correlation: Quantifying Relationships

Covariance and correlation are key measures for quantifying the relationship between two variables. Covariance indicates the direction of the relationship, while correlation standardizes this measure, making it easier to interpret the strength of the association. These metrics lay the groundwork for predictive modeling. Understanding relationships between variables is crucial in statistical analysis.

Covariance

Covariance indicates the direction of the linear relationship between two variables:

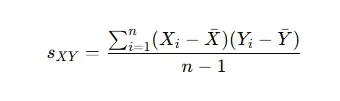
Correlation Coefficient

The correlation coefficient (rr) normalizes covariance to a scale of -1 to 1, showing the strength of the relationship:

Correlation:

A high absolute value of rr indicates a strong linear relationship.

Where:

• sXY is the covariance between X and Y.
• sX is the standard deviation of X.
• sY is the standard deviation of Y.
• rr is the correlation coefficient.

3. Regression Analysis: Building Predictive Models

Regression analysis is a powerful tool for modeling relationships between variables. Using methods like Ordinary Least Squares (OLS), you can estimate coefficients that describe how changes in independent variables influence the dependent variable. Regression models enable both prediction and explanation, offering actionable insights. Regression analysis aims to model the relationship between dependent (YY) and independent (XX) variables.

Ordinary Least Squares (OLS) Method

The OLS method minimizes the sum of squared residuals to estimate the slope (β1) and intercept (β0):

where sXY is the covariance between X and Y, and s(2/X) is the variance of X.

Predicted Values and Residuals

Predicted values (Y^i)are computed as

Residuals (uiu_i) measure the deviation of actual values from predicted values:

The goal of OLS is to minimize the residual sum of squares (RSS):

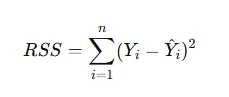
Residual analysis is crucial for assessing model fit, as it helps identify patterns or violations of assumptions, such as non-linearity or heteroscedasticity, that may impact the reliability of the regression model.

4. Visualizing Data and Regression Results

Graphs and plots are invaluable for presenting data and regression outcomes. Scatterplots with regression lines illustrate relationships effectively, while residual plots help assess model fit. Visualization enhances understanding and communicates findings clearly. Graphical representation is an effective way to interpret and communicate findings. For assignments involving regression:

• Scatterplots: Show the relationship between XX and YY.
• Regression Line: Overlay the best-fit line derived from OLS estimates.
• Annotations: Label key components such as data points, regression equations, and axes.

Visualization helps validate the linearity assumption and identify potential outliers.

5. Estimation: Unbiased and Efficient Estimators

Estimators play a crucial role in statistical analysis. An unbiased estimator ensures accuracy, while efficiency minimizes variance, enhancing reliability. Techniques like weighted averages can further optimize estimators for specific scenarios, improving analytical outcomes. Assignments may also delve into theoretical aspects of estimation, such as unbiasedness and efficiency.

Unbiased Estimators

An estimator is unbiased if its expected value equals the population parameter. For example, the sample mean (Xˉ) is an unbiased estimator of the population mean (μ\mu).

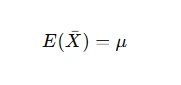
Variance of Estimators

Efficiency relates to the variance of an estimator. A lower variance indicates greater precision. For weighted averages, the choice of weights affects the estimator’s variance:

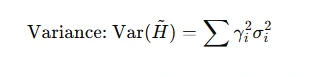
Optimal Weights

The optimal weights for minimizing variance can be derived using:

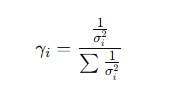
Substituting these weights into the variance formula results in the minimized variance of the weighted average:

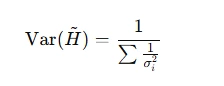
By ensuring unbiasedness and selecting optimal weights, estimators can achieve both accuracy and precision, providing robust solutions in statistical analysis.

6. Conditional Expectations and Linear Relationships

Conditional expectations describe the expected value of one variable given another. Linear relationships simplify this concept, allowing for straightforward interpretations. These tools are integral for understanding dependencies in data, aiding in sound decision-making. Conditional expectations are frequently explored in assignments involving predictive models. For example, the conditional expectation of GPA given SAT scores follows a linear equation:

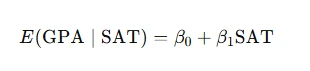
This relationship can be extended to interpret results in regression problems.

7. Practical Tips for Solving Statistical Assignments

To excel in statistical assignments, break the problem into smaller tasks, leverage tools like spreadsheets, and verify calculations step-by-step. Staying organized and documenting methods ensures reproducibility and accuracy. Seeking guidance or reviewing theoretical concepts can also clarify challenging aspects.

1. Read Instructions Carefully: Identify key tasks and required outputs.
2. Organize Data: Ensure data is clean and correctly formatted for analysis.
3. Use Appropriate Tools: Leverage calculators, spreadsheets, or statistical software for computations.
4. Follow Step-by-Step Methods: Break down calculations into manageable steps.
5. Interpret Results: Go beyond computation to explain findings and their implications.
6. Check Assumptions: Validate assumptions like linearity and independence.
7. Review Work: Double-check calculations and ensure clarity in graphical and written outputs.

Conclusion

Solving statistical assignments involves a blend of theoretical understanding and practical application. By mastering the concepts of descriptive statistics, covariance, correlation, regression analysis, and unbiased estimation, students can confidently tackle assignments like the one discussed here. Focus on clarity, precision, and interpretation to produce comprehensive and accurate solutions.