+1 (315) 557-6473 

Statistical Analysis Case Study: Correlation & Regression

In this Regression Analysis assignment, we explore correlation and regression analysis. We begin with correlation analysis, examining the relationship between variables, followed by interpreting the results. Then, we delve into a case study to understand the correlation between achievement test scores and academic GPA. Finally, we discuss the fundamentals of regression analysis.

  1. Home
  2. A Case Study on Correlation & Regression Analysis

Problem Description:

The primary focus is on conducting a correlation analysis using statistical data. The problem statement revolves around the examination of the relationship between two continuous variables: the Second-Year OMM Written Examination score and the Complex-USA Level 1 Total Score. Students are required to assess the strength and significance of this correlation, interpret its implications, and perform regression analysis. Additionally, students must analyze a case study involving the prediction of standardized test scores using GPA. The aim is to evaluate students' understanding of correlation analysis, regression, and data interpretation in a real-world context, ultimately demonstrating their ability to apply statistical concepts to practical scenarios.

Solution

CORRELATION ANALYSIS:

Statistical Association: Statistical Association describes the relationship between what types of variables?

Ans: Continuous Variables

Use the figure below for next six questions

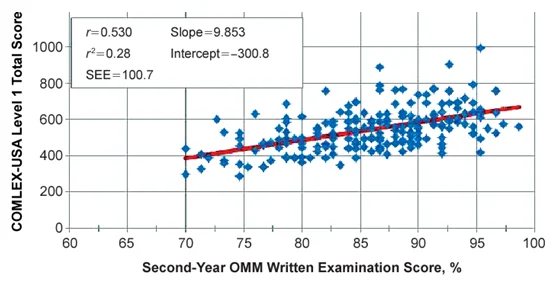
Second Year OMM Written Examination Score

Independent Variable & Scale of Measurement: What is the independent variable & its scale of measurement? Ans: The independent variable is the Second-Year OMM Written Examination score, measured at an Interval scale.

Dependent Variable & Scale of Measurement: What is the dependent variable & its scale of measurement? Ans: The dependent variable is the Complex-USA Level 1 Total Score, measured at an Interval scale.

r Value & Interpretation: What is the r value? What does it tell us? Ans: The r-value is 0.53, indicating a moderate linear association between the Second-Year OMM Written Examination score and Complex-USA Level 1 Total Score. The correlation suggests that as the OMM score increases, the Complex-USA Level 1 Total Score also tends to increase.

r2 Value & Interpretation: What is the r2 value? What does it tell us? Ans: The r2 value is 0.28, indicating that 28% of the variation in the Complex-USA Level 1 Total Score can be explained by the Second-Year OMM Written Examination score.

Predicting OMM Score: Predict what OMM score is needed to obtain a COMLEX score of 600. Ans: An OMM score of 91.42 is needed to obtain a COMLEX score of 600 based on the provided model.

Using COMLEX Scores to Predict OMM Score: Should you use COMLEX scores to predict what a student’s OMM score was? Why or why not? Ans: No, COMLEX scores should not be used to predict a student's OMM score due to the poor performance of the model as indicated by the low r2 value.

Decision Tree: Regarding the Decision tree:

Fill in any missing blanks

Ans:

  1. Comparing two or more quantitative variables
  2. Correlation and Regression
  3. 1 sample t-test
  4. Paired or related samples
  5. Independent student t-test, Confidence Intervals, or Mann-Whitney U-test

Study Abstract:

Variables: What are the variables the study is looking at?

Ans: The variables studied are teaching evaluation scores, student’s final grades, and course fail rates.

Correlation Analysis Assumptions:

  • What are the assumptions in conducting a correlation analysis?

Ans:

  • Both variables must be continuous.
  • There should be no outliers in the variables.
  • A linear relationship between the two variables must exist.

Meeting Assumptions:

  • Did this study meet those assumptions, based on the abstract provided? Ans: Yes, the study met the assumptions.

Causation Elements:

  • Describe the required elements for causation. Ans: Causation requires Temporal precedence, Empirical association, and Nonspuriousness to be satisfied.

Study's Conclusion:

  • Did this study conclude that one variable caused another to occur? Ans: Yes, the study concluded that students’ final grades have an effect on the teaching evaluation scores.

Results Table:

Covariance Definition:

Define covariance: Ans: Covariance is a measure of how two random variables in a data set change together.

Variables for Covariance: Based on the table and abstract provided earlier in the assignment, what are the two variables associated with covariance for this study? Ans: The variables associated with covariance are teaching evaluation scores and student’s final grades.

r Value for 2014: What is the r value for teaching evaluations linking to each student’s grade in 2014? Ans: The r value for 2014 is 0.080.

Sign of Correlation Coefficient: What does the sign of this correlation coefficient indicate in relation to the study and abstract? Ans: The positive sign indicates a positive correlation between teaching evaluation scores and students’ final grades in 2014.

Statistical Significance: Is the r value for teaching evaluation scores linked to whole class average grades statistically significant? If yes, what is the p value less than? Ans: Yes, the r value for teaching evaluation scores linked to whole class average grades is statistically significant with a p-value less than 0.001.

Graph Analysis:

Weakest Correlation:

  • Which graph below depicts the weakest correlation? Ans: Graph C depicts the weakest correlation.

Strongest Correlation:

  • Which graph below depicts the strongest correlation? Ans: Graph A depicts the strongest correlation.

Graph A's Correlation: Is graph A depicting a positive or negative correlation? Ans: Graph A depicts a positive correlation.

REGRESSION ANALYSIS:

Comparison of Regression Types: Compare and contrast simple linear regression, multiple regression, and logistic regression. Ans: (Explanation provided)

Main Symbol for Regression Output: What is the main symbol for output of regression analysis and what does it tell us? Ans: The main symbol is Y, representing the value for each respective observation.

Simple Linear Regression Formula: List the formula for simple linear regression and describe what each variable stands for. Ans: (Formula and explanation provided)

CASE STUDY (USE EXCEL):

Calculating r: Calculate the value of r using Excel. Ans: The r value is 0.524.

Interpreting r: Interpret the value of r in terms of the hypothesis. Ans: The value indicates a moderate linear relationship between achievement test scores and class performance.

Predicting Test Score: If you wanted to predict a student’s standardized test score using their GPA, what statistical analysis would you use? Ans: Regression Analysis

Intercept and Slope: To get the y-intercept and slope, use Excel. Ans: (Values provided)

Predicted Test Score: Insert the values into the equation and determine what test score is expected if a student has a GPA of 3.8. Ans: (Calculation and answer provided)

R2 Calculation: What proportion of variation in standardized test scores is explained by GPA? What is the R2 value? Ans: (R2 value and interpretation provided)

Scatterplot: Using Excel, create a scatterplot of the case study data. Ans: (A screenshot is required.)