Performing Principal Component Analysis In R

Our top-rated experts have used their expertise in R programming to analyze intricate relationships among various economic variables and harness the power of Principal Component Analysis (PCA) to uncover the underlying structure within the data. Our exploration begins by examining the correlation between eight economic variables: Food, Cloth, Resid, HousF, Health, TranC, Educ, and Miscel.

Problem Description:

The aim of Principal Component Analysis In R homeworkis to explore the relationships between various economic variables and perform Principal Component Analysis (PCA) to understand the underlying structure of the data. Our dataset consists of eight economic variables: Food, Cloth, Resid, HousF, Health, TranC, Educ, and Miscel.

Solution

1(a). Correlation between variables:

Food Cloth Resid HousF Health TranC Educ Miscel

Food 1

Cloth 0.26 1

Resid 0.71 0.4 1

HousF 0.72 0.45 0.77 1

Health 0.39 0.58 0.69 0.58 1

TranC 0.9 0.36 0.79 0.78 0.47 1

Educ 0.83 0.54 0.81 0.89 0.63 0.88 1

Miscel 0.72 0.63 0.72 0.72 0.63 0.75 0.84 1

P-VALUE OF CORRELATION MATRIC

Food Cloth Resid HousF Health TranC Educ Miscel

Food 0.1626 0.0000 0.0000 0.0324 0.0000 0.0000 0.0000

Cloth 0.1626 0.0239 0.0103 0.0007 0.0481 0.0016 0.0002

Resid 0.0000 0.0239 0.0000 0.0000 0.0000 0.0000 0.0000

HousF 0.0000 0.0103 0.0000 0.0006 0.0000 0.0000 0.0000

Health 0.0324 0.0007 0.0000 0.0006 0.0081 0.0002 0.0002

TranC 0.0000 0.0481 0.0000 0.0000 0.0081 0.0000 0.0000

Educ 0.0000 0.0016 0.0000 0.0000 0.0002 0.0000 0.0000

Miscel 0.0000 0.0002 0.0000 0.0000 0.0002 0.0000 0.0000

Interpretation: There is significant correlation between all variables except food and cloth.

b) For principal component analysis either covariance matric or correlation matrix is possible. The difference between them is only in data pre-processing. If the matrix is centered but not scaled, its PCA of the covariance matrix. The PCA of correlation matrix was computed as singular value decomposition of column centered, scaled matrix.

For this assignment let proceed to – PCA with correlation matrix

c) Result of performed PCA using R

PC1 PC2 PC3 PC4 PC5

Food -0.3529911 0.42928651 -0.17543240 0.29872838 -0.00560897

Cloth -0.2495530 -0.67695648 -0.52091532 -0.09658973 0.39814884

Resid -0.3709478 0.05620474 0.44150056 0.07047522 0.58892053

HousF -0.3738247 0.08844179 0.07324417 -0.78940954 -0.25985063

Health -0.3015777 -0.47168317 0.62781292 0.22597502 -0.25311203

TranC -0.3760828 0.32419614 -0.12268623 0.12654342 0.27873101

Educ -0.4040119 0.06966587 -0.08995771 -0.19992907 -0.13226521

Miscel -0.3743799 -0.11840869 -0.28335470 0.40773524 -0.51753796

PC6 PC7 PC8

Food 0.37675460 -0.65134636 0.06976856

Cloth 0.13320574 -0.13409455 0.06725512

Resid -0.53048320 -0.16662669 -0.05783575

HousF -0.06553027 -0.11670387 0.37210836

Health 0.41323273 0.03605416 0.07228562

TranC 0.27077814 0.69470347 0.29794079

Educ 0.08592665 0.15644120 -0.85703307

Miscel -0.55058159 0.08941841 0.14247766

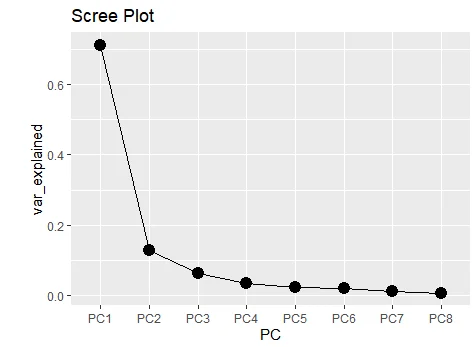
d) What percentage of variability explained by each PCA? Also cumulative percentages of variance? also scree plot?

Importance of components:

PC1 PC2 PC3 PC4 PC5 PC6

Standard deviation 2.3877 1.0141 0.71026 0.5223 0.43138 0.40171

Proportion of Variance 0.7127 0.1286 0.06306 0.0341 0.02326 0.02017

Cumulative Proportion 0.7127 0.8412 0.90426 0.9384 0.96163 0.98180

PC7 PC8

Standard deviation 0.29539 0.24157

Proportion of Variance 0.01091 0.00729

Cumulative Proportion 0.99271 1.00000

PC1 explained 71.27% of variance, PC2 explained 12.86%of variance.

Cumulative percentages of variance or proportion of PC1 and PC2 explained is 84.12%

e) linear combination of original data

PC1 = -0.35Food -0.24Cloth -0.37HousF – 0.30Health -0.37TranC – 0.40 Educ- 0.37 Miscel

Educ, Miscel, TranC, HousF has biggest role in the construction of PC1

PC2 = 0.42 Food – 0.67 Cloth + 0.05Resid + 0.08 HousF – 0.47Health + 0.32 TranC + 0.06Educ – 0.11Miscel

Cloth,Food,Health has biggest role in the construction of PC2.

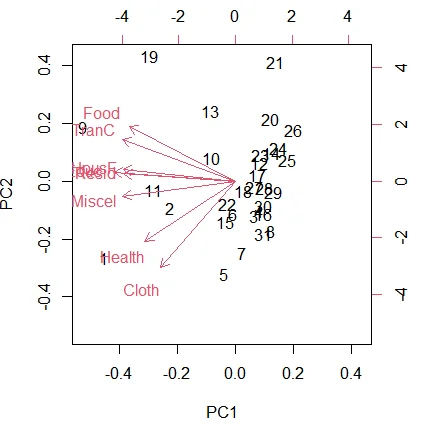
f) Biplot of the first 2 PCA